基本概念

模态分析

模态分析是研究结构动力特性一种方法，一般应用在工程振动领域。

其中，模态是指机械结构的固有振动特性，每一个模态都有特定的固有频率、阻尼比和模态振型。分析这些模态参数的过程称为模态分析。

按计算方法，模态分析可分为： * 计算模态分析：由有限元计算的方法取得待识别参数 * 试验模态分析：通过试验将采集的系统输入与输出信号经过参数识别获得待识别参数

通常，模态分析都是指试验模态分析。

实验模态分析

实验模态分析主要是通过模态试验，测量系统的振动响应信号或同时测量系统的激励信号和响应信号，从测量信号中，识别描述系统动力特征的有关参数。

试验模态分析结果可以验证和修改结构数学模型、综合试验分析模型、校核动态计算分析结果的有效性、分析结构产品性能、检查结构中的薄弱部位、鉴定结构总体设计的合理性。

待识别参数

• 物理参数：质量矩阵、刚度矩阵、阻尼矩阵等
• 模态参数：固有频率、衰减系数、模态矢量、模态刚度、模态阻尼

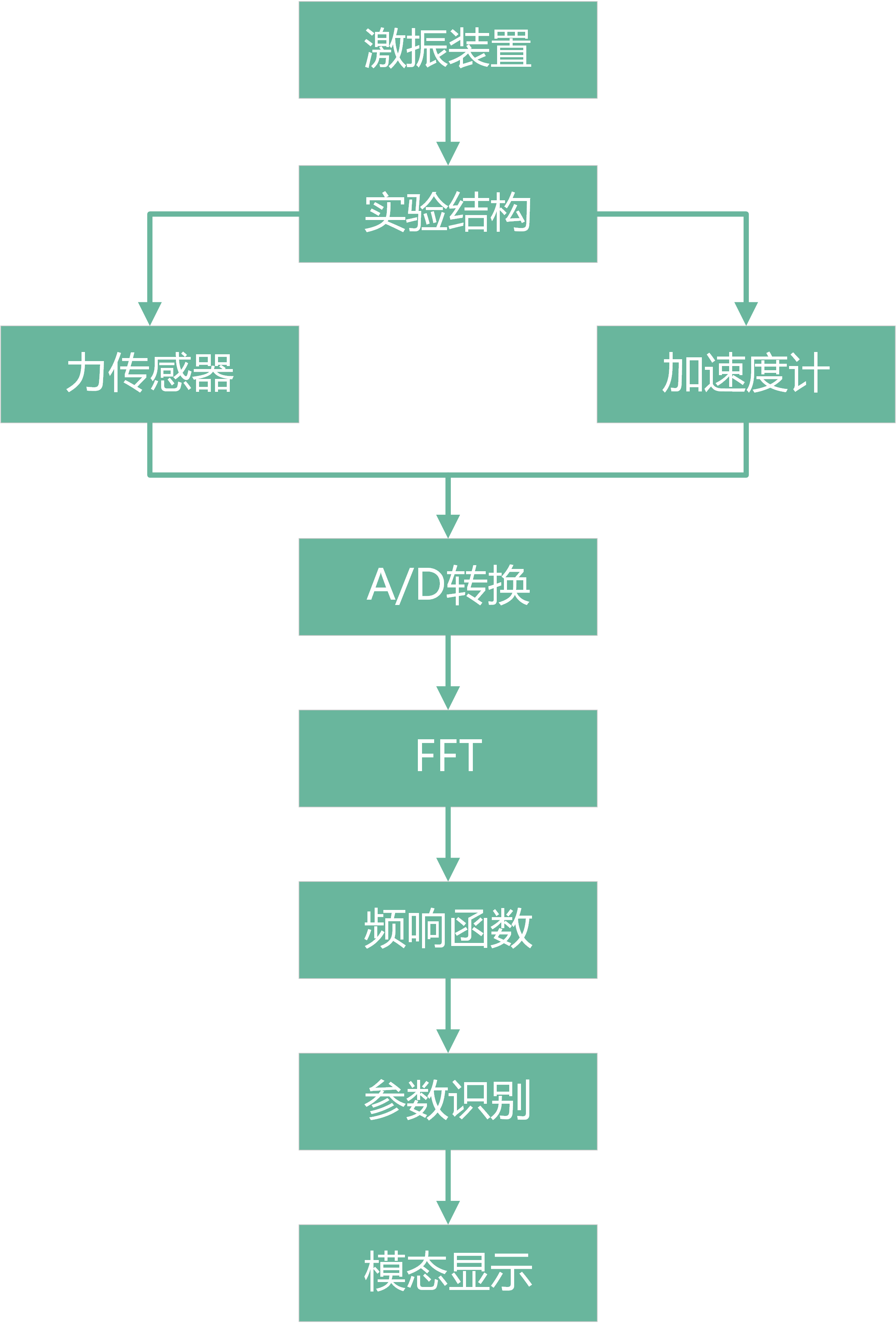
模态分析系统的组成

• 激振系统：使得系统产生稳态、瞬态或随机振动
  • 稳态正弦激振法
  • 瞬态激振法
    • 快速正弦扫描激振法
    • 脉冲锤击激振法
  • 随机激振法
    • 纯随机激振法
    • 伪随机激振法
    • 周期随机激振法
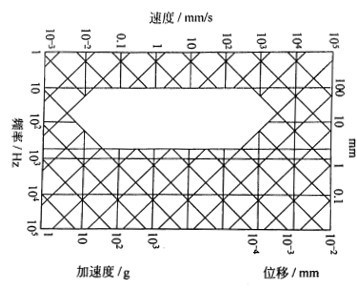
• 测量系统：用传感器测量实验对象的各个主要部位上的位移、速度或加速度信号，然后将这些信号与激振信号一起记录并保存
• 分析系统：将保存的激励信号和响应信号经过数模转换，采样并输入数字式分析仪或计算机中，用硬件或软件系统识别振动系统的模态参数

实验模态分析的基本原理

基本原理

本部分以多自由度动力学系统为例，阐明了实验模态分析的基本原理： 对于多自由度动力学常微分方程 \(\rightarrow\) 对其拉氏变换 \(\rightarrow\) 得到传递函数 \(\rightarrow\) 通过振型的正交性 \(\rightarrow\) 发现传递函数中含有模态参数的信息 \(\rightarrow\) 因此可以通过实验可以得到传递函数 \(\rightarrow\) 再从传递函数中识别得到振动系统有关参数 \(\rightarrow\) 最后进一步计算得到待求模态参数

传递函数与模态参数的关系

对于多自由度动力学系统，其动力学方程为：

\[ \textbf{M}\bar{\ddot{x} }+\textbf{C}\bar{ \dot{x} }+\textbf{K}\bar{x}=\bar{f} \]

对其进行拉氏变换：

\[ \textbf{M}\left[ s^2 \bar{X}(s) - s\bar{x}(0) - \bar{\dot{x} }(0) \right] + \textbf{C} \left[ s\bar{X}(s) - \bar{x}(0) \right] + \textbf{K} \bar{X}(s) = \bar{F}(s) \]

初始条件全为0时：

\[ \left[ s^2 \textbf{M} + s \textbf{C} + \textbf{K} \right] \bar{X}(s) = \bar{F}(s) \]

根据传递函数的定义，系统的传递函数为：

\[ \textbf{H}(s)=\frac{\bar{X}(s)}{\bar{F}(s)} = \frac{ 1}{ s^2 \textbf{M} + s \textbf{C} + \textbf{K} } \]

机械系统中传递函数的定义：零初始条件下线性系统响应（即输出）量的拉普拉斯变换与激励（即输入）量的拉普拉斯变换之比。

利用振型的正交性，当模态振型矩阵为$ [] $时，模态质量矩阵、模态阻尼矩阵、模态刚度矩阵为：

\[ \textbf{M}_r = [\varphi]^\mathrm{T}\textbf{M}[\varphi] = \mathrm{diag}(m_1 \, \cdots \, m_r \, \cdots \, m_N) \]

\[ \textbf{C}_r = [\varphi]^\mathrm{T}\textbf{C}[\varphi] = \mathrm{diag}(c_1 \, \cdots \, c_r \, \cdots \, c_N) \]

\[ \textbf{K}_r = [\varphi]^\mathrm{T}\textbf{K}[\varphi] = \mathrm{diag}(k_1 \, \cdots \, k_r \, \cdots \, k_N) \]

将上式代入传递函数，可得到：

\[ \textbf{H}(s)= [\varphi] \left[ s^2 \textbf{M}_r + s \textbf{C}_r + \textbf{K}_r \right]^\mathrm{-1}[\varphi]^\mathrm{T} \]

将传递函数矩阵展开可以发现，它的每一行或每一列都包含有所有的模态信息：模态质量矩阵、模态阻尼矩阵、模态刚度矩阵中所有元素以及所有模态矢量。

实验、传递矩阵和模态参数的关系

若固定在一点测量振动响应信号，而不断改变激励信号的作用点，这样就测量出了传递函数的一行；若固定在一点进行激励，而在不同点进行振动响应信号测量，这样就测量出了传递函数的一列。

从上一节的分析中可知，传递函数矩阵的每一行或每一列都包含有所有的模态信息。因此，只要通过实验测得传递函数矩阵的一行或一列再加以分析计算，就可以得到全部的模态信息。

从传递函数中求出模态参数的方法，被称为参数识别方法。一般通用的参数识别方法有两种：图解法和曲线拟合法。

• 图解法是利用频响函数曲线直接进行模态识别的方法。其优点是简便、直观，缺点是精度差、不能排除外界干扰。

• 曲线拟合法是用一条连续曲线去拟合一组离散的实验数据，然后利用拟合曲线识别有关参数的方法。该方法常利用图解法所识别的参数作为初始值进行迭代优化计算，直到满足精度为止，从而可以从传递函数中识别得到振动系统有关参数，最后进一步计算得到待求模态参数。

实验模态分析的主要过程

根据实验模态分析的基本原理，现将实验模态分析的主要过程总结如下： 1. 确定实验模型，将实验结构支撑起来（边界条件的确定） 1. 进行模态试验，利用上述激振方法进行激励实验结构（一般用锤击法），记录原点和各测点的激励、响应时间历程曲线 1. 对各测点的时间历程数据进行数字处理，利用传递函数与模态参数的关系和时/频域转换技术求出各测点的传递函数，并组成传递函数矩阵 1. 利用参数识别方法进行参数识别，求得模态参数 1. 进行模态动画展示

灵敏度

灵敏度是指沿传感器的测量方向，对应于每一单位简谐机械量的输入，其开路时电信号的输出，即输出比输入。

• 输入的机械量：\(x=X\sin(\omega t +\alpha)\)
• 输出的电信号：\(e=E\sin (\omega t+ \alpha - \theta)\)，\(\theta\) 为相移，即输出的电信号\(e\)对被测机械量\(x\)的相位滞后
• 灵敏度：\(s=E/X\) （电信号单位 / 机械量单位）

通常，\(X\) 是位移、速度、加速度、力、应变等，\(E\) 是电压、电荷等。

分辨率

分辨率是指传感器可感受到的被测量的最小变化的能力。

也就是说，如果输入量从某一非零值缓慢地变化，但变化值未超过某一数值 \(\Delta X\) 时，传感器的输出变化量 \(\Delta E =0\) ，即传感器对此输入量的变化是分辨不出来的。只有当输入量的变化超过分辨率时，其输出才会发生变化。

\(\Delta X\) 越小，灵敏度越高，分辨率也越高。灵敏度越高，传感器的信噪比将相应下降，这将降低测量结果的精度，故应综合考虑。

线性度和线性范围

通常情况下，传感器的实际静态特性输出是条曲线而非直线。在实际工作中，为使仪表具有均匀刻度的读数，常用一条拟合直线近似地代表实际的特性曲线。

线性度（非线性误差）\(\gamma\) 就是这个近似程度的一个性能指标，定义为在全量程范围内实际特性曲线与拟合直线之间的最大偏差值与满量程输出值之比。

\[ \gamma=\frac{ \Delta E }{ E_{max} - E_{min} } \times 100 \\% \]

线性范围是指传感器测量量与实际被测量之间保持近似线性关系的范围。

频率范围

频率范围是指传感器的灵敏度随频率的变化量不超出某一给定的误差限的频率范围（频率上限和下限）。传感器的频率范围取决于： 1. 机械接收部分的频率特性。 1. 机电变换部分和所用二次仪表的频率特性。 1. 传感器的安装条件也影响频率上限。

备注： * 在制定测量方案时，首先要看传感器的频率范围是否满足测量的要求 * 压电式加速度传感器具有较宽的频率范围，而且频率上限也比较高 * 电阻式、压阻式和伺服式等三种加速度传感器都具有零频率响应，其中压阻式也具有较高的上限频率

固有频率与安装谐振频率

对于惯性式接收传感器，其机械接收部分是由质量块、阻尼器、弹簧构成的单自由度振动系统，其质量、阻尼、刚度分别为 \(m, c, k\)。该振系统无阻尼自由振动的频率 $ _n = $ 被称为传感器的固有频率。

传感器产生共振时的最低频率称为安装谐振频率，若安装刚度是有限的（实际上也很难达到无穷大），则其对传感器的接收特性将有较大影响。

工作范围

频率范围和线性范围一起决定了传感器的工作范围。工作范围可以从诺谟图（Nomogram）中得到

横向灵敏度与方向特性

横向灵敏度主要是由于最大灵敏度轴与传感器的几何轴线不重合而引起的。这是由于传感器加工、安装上的间歇误差等条件造成的。最大灵敏度的轴线与几何轴线间的夹角为 \(\theta\)，最大的横向灵敏度表示为：

\[ s_t=\tan \theta \]

备注： * 加速度传感器的外壳上的红点被用来表示横向灵敏度的方向。 * 一般令红点和传感器中心的连线，与振幅最大的非被测振动方向垂直，以减少测量误差。

动态范围

动态范围是指某一输入机械量的幅值范围（用分贝表示），该范围内传感器的灵敏度随输入机械量幅值的变化量不超出某一给定的误差限。

\[ D=20 \lg \frac{X_{max}}{X_{min}} \]

动态范围越大，说明传感器对幅值变化的适应能力越强。比如 \(D=80dB\)，则幅值上限与下限之比达10000倍。传感器的量程即是指其幅值上限与下限值的代数差。

其他

传感器的其它性能参数还包括其质量、重复性、稳定性、输入输出阻抗、阻尼、迟滞、零飘、过载能力、以及它的工作环境条件等。

采样

采样就是将连续模拟信号变为离散数字信号的过程。

什么是采样定理

离散后的信号能唯一的确定原连续信号，并要求离散信号通过D/A（数/模）转化后能恢复成原连续信号。由于离散信号是从连续信号上取出的一部分值，与连续信号的关系是整体和局部的关系，一般来说是不可能唯一确定连续信号的。只有在满足一定条件下，离散信号才可按照一定方式恢复出原来的连续信号。这个条件就是采样定理。

如何满足采样定理

采样定理：采样频率必须大于被分析信号成分中最高频率值的两倍以上，否则将产生高、低频混淆现象，即高频信号经采样后只出现低频信号，采样信号无法还原为原信号。 \[ f_s=\frac{1}{\Delta t} >2f_m \]

其中\(f_s\)是采样频率，\(f_m\)是被分析信号成分中的最高频率值，\(\Delta t\)是采样时间间隔。

频率混淆现象

如果想彻底了解采样定理的内涵，以及为什么不满足采样定理就会出现混淆现象，请接着看下去 读者自己推导采样后得到的信号\(x_s(t)\)的傅里叶变换表达式\(X_s(j\omega)\)，再根据\(X_s(j\omega)\)绘制频谱图，最终就会理解采样定理的内涵。

为了便于推导，现定义： * 原信号：\(x_m(t)\)，傅里叶变换后为\(X_m(j\omega)\) * 采样函数：\(s(t)\)，傅里叶变换后为\(S(j\omega)\) * 采样后输出信号：\(x_s(t)\)，傅里叶变换后为\(X_s(j\omega)\)

采样函数\(s(t)\)

当我们把采样的过程看作一个周期为 \(T\) 、宽度为 \(\tau\) 的矩形脉冲信号\(s(t)\)。当\(\tau\ll T\) 时，采样脉冲信号\(s(t)\)具有了狄拉克\(\delta\)函数的性质：

\[ \delta(t)= \begin{cases} \infty & t=0 \\\\ 0 & t\neq 0 \end{cases} \]

\[ s(t)= \sum^\infty_{n=-\infty} \delta(t-nT) \]

为了便于傅里叶变换，把\(s(t)\)表示为傅里叶级数的形式：

\[ s(t)=\sum^\infty_{k=-\infty} a_k e^{jk\omega_s t} ,\quad \omega_s=\frac{2\pi}{T} \]

其中：

\[ a_k=\frac{1}{T} \int^{T/2}_ {-T/2} \sum\nolimits^\infty_{n=-\infty} \delta(t-nT) e^{-j\omega_s t} dt=\frac{1}{T} \]

因此，有：

\[ s(t)=\frac{1}{T} \sum^\infty_{k=-\infty} e^{jk\omega_s t} \]

对\(s(t)\)进行傅里叶变换得到\(S(j\omega)\)：

\[ S(j\omega)=F \left[ s(t) \right] =F \left[ \frac{1}{T} \sum^\infty_{k=-\infty} e^{jk\omega_s t} \right] = \frac{1}{T} \sum^\infty_{k=-\infty} F \left[ e^{jk\omega_s t} \right] \]

查常用Fourier变换表可知：

\[ F \left[ e^{jk\omega_s t} \right] =2\pi \delta(\omega -k\omega_s) \]

则\(S(j\omega)\)为：

\[ S(j\omega) = \frac{2\pi}{T} \sum^\infty_{k=-\infty} \delta(\omega -k\omega_s) \]

采样后输出的信号\(x_s(t)\)

采样后输出的信号\(x_s(t)\)等于原信号\(x_m(t)\)乘采样函数\(s(t)\)：

\[ x_s(t)=x_m(t)s(t) \]

记\(*\)为卷积，根据频域下的卷积定理

\[ f_1(t)f_2(t)=\frac{1}{2\pi}F^{-1}\left[ F_1(j\omega)* F_2(j\omega)\right] \]

采样后输出的信号\(X_s(j\omega)\)为：

\[ X_s(j\omega)=\frac{1}{2\pi} X_m(j\omega)*S(j\omega)=\frac{1}{2\pi}· X_m(j\omega) *\left[ \frac{2\pi}{T} \sum^\infty_{k=-\infty} \delta(\omega -k\omega_s) \right] \]

根据冲击函数的性质有： \[ X_s(j\omega)=\frac{1}{T} \int^\infty _ {-\infty} X_m(j\theta) \sum^\infty_{k=-\infty} \delta(\omega -k\omega_s - \theta) d\theta \]

冲激函数的性质：\(f(t)*\delta(t-t_0)=f(t-t_0)\)

最终，采样后信号的傅里叶变换为：

\[ X_s(j\omega)=\frac{1}{T}\sum^\infty_{k=-\infty} X_m(j\omega-jk\omega_s) \]

从上式可以看出，原信号的频谱\(X_m(j\omega)\)在频域内发生了周期延拓。即，原信号在频谱上的宽度是\(2f_m\)，每隔\(f_s\)重复一次（相当于信号的平移），发生了周期延拓，从图中直观的看出来，如果\(f_s<2f_m\)，延拓后的信号会在频域内会发生混淆。

压电效应

某些电介质在沿一定方向上受到外力的作用而变形时，其内部会产生极化现象，同时在它的两个相对表面上出现正负相反的电荷。当外力去掉后，它又会恢复到不带电的状态，这种现象称为正压电效应。当作用力的方向改变时，电荷的极性也随之改变。依据电介质压电效应研制的一类传感器称为压电传感器。

压电加速度传感器

压电式加速度传感器又称压电加速计。 工作原理：在加速度计受振时，质量块加在压电元件上的力也随之变化。当被测振动频率远低于加速度计的固有频率时，则力的变化与被测加速度成正比。压电式加速度传感器利用了某些物质的压电效应，可以将加在自身上的力转化为电荷的变化，即将机械信号转化为电信号，进而通过电信号的转化成功输出或储存被测物体的加速度信号。

设 \(q\) 为释放的电荷，\(F\) 为作用力，\(A\) 为电极化面面积，\(d_x\) 是压电系数，单位为 \(C/N\)（库伦/牛），则下列关系式成立：

\[ \frac{q}{A}=d_x\frac{F}{A} \]

理论与试验研究表明，在一般情况下，表示机械量和电量之间关系的压电方程是很复杂的，但是在压电材料弹性变形范围内，电荷与作用力之间的关系可以用线性映射关系表现出来:

\[ \bar{q}=\textbf{D}\bar{F} \]

如上所示，压电型加速度传感器，基座受到的加速度最终会以电压形式输出。电荷及电压输出都与加速度成一定比例关系，因此通过测量电荷和电压即可得出加速度。一般电荷输出称为电荷灵敏度，电压输出称为电压灵敏度。

Markdown基本语法

标题

添加标题：在文本前加#，#的数目代表标题的级别，最高支持六级标题

1
2
3
4
5
6

# 一级标题
## 二级标题
### 三级标题
#### 四级标题
##### 五级标题
###### 六级标题

1
2
3
4

*被添加斜体的文本*  
**被加粗文本**
***被倾斜加粗的文本***
~~被加删除线的文本~~

分割线

在空行内输入---或___或***即可，符号中间也可插入空格。效果如下：

引用

在被引用的文字前加>

1
2
3

>这是一段引用内容，它很长很长很长很长很长很长很长------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
>
>这是第二段引用内容，它很短

也可以控制引用的级别，>的个数代表级别

1
2
3

>一级文本：对于命途多舛的人生，以及渺茫的时间，阻挡在我们之间这一事实，我们无可奈何。
>>二级文本：彼方为谁，无我有问。九月露湿，待君之前。
>>>三级文本：但盼风雨来、能留你在此;即使天无雨、我亦留此地。

1
2
3

- Harry James Potter
* Hermione Jean Granger
+ Ronald Bilius "Ron" Weasley

有序列表使用1.，即任意数字加英文句号进行标记，并且数字不影响最终编译效果。

1
2
3

1. Albus Percival Wulfric Brian Dumbledore
8. Severus Snape
10. Minerva McGonagall

列表可以嵌套 在上一级与下一级列表之间敲三个空格即可。

1
2
3
4
5

* Lord Voldemort
    * Lupin
    * Dobby
        * Winky
        * Tom Riddle 

1
2
3
4
5

1. Lord Voldemort
    1. Lupin
    1. Dobby
        1. Winky
        1. Tom Riddle 

效果演示： 1. Lord Voldemort 1. Lupin 1. Dobby 1. Winky 1. Tom Riddle

列表包含多个段落 列表包含多个段落，每个项目下的段落都缩进4个空格或一个制表符。

1
2

*   Harry Potter, Protagonist, is a thin, black-haired youth wearing glasses on his forehead with a lightning-shaped scar, just as suddenly a short time overstating the children who, like flavor is not good. 
    He is a Magic School fifth-grade students, but also a man of Hogwarts. Since Voldemort after the resurrection, the scar on his forehead to his burning often endless.

代码

在行内插入简短的代码 把代码插入``之间即可

1

看起来`codes and codes`是这样的

在行间插入代码块 把代码块放入两行```之间(\是为了防止转义，实际写作中是没有的)

1
2
3
4
5

\```
start
codes and codes
end
\```

1
2
3

start
codes and codes
end

强制空行

在空行内使用\即可

1
2
3
4

第一段
\
\
第二段