数学概念——同伦
概念
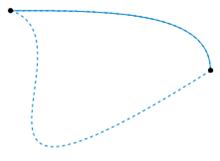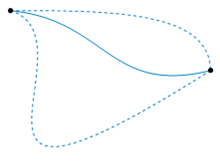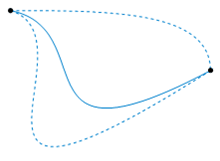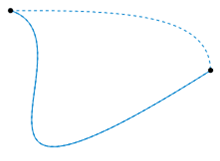
同伦:在数学和拓扑学上描述了两个对象间的“连续变化”。
两个定义在拓扑空间之间的连续函数,如果其中一个能“连续地形变”为另一个,则这两个函数称为同伦的。这样的形变称为两个函数之间的同伦。
定义
给定两个拓扑空间 \(X\) 和 \(Y\)。考虑两个连续函数 \(f, g: X\rightarrow Y\),若存在一个定义在空间 \(X\) 与单位区间 \([0,1]\) 的积空间上的连续映射 \(H: X \times [0,1] \rightarrow Y\) 使得:
- \(\forall x \in X, H(x,0)=f(x)\)
- \(\forall x \in X, H(x,1)=g(x)\)
则称 \(H\) 是 \(f, g\) 之间的一个同伦。
如果我们将 \(H\) 的第二个参数当作时间,这样 \(H\) 相当于描述了一个从 \(f\) 到 \(g\) 的连续形变: 0 时刻得到函数 \(f\),1时刻得到函数 \(g\), 反之亦然。
