转动惯量/截面惯性矩/极惯性矩
转动惯量
概念
在经典力学中,转动惯量又称惯性矩(英语:moment of inertia, mass moment of inertia, second moment of mass, 最准确的表达应该是 rotational inertia),通常以 \(I\) 表示,国际单位制为 \(kg \cdot m^2\)。
转动惯量是一个物体对于其旋转运动的惯性大小的量度。一个刚体对于某转轴的转动惯量决定对于这物体绕着这转轴进行某种角加速度运动所需要施加的力矩。
定义
对于刚体,其转动惯量由积分表示: \[ I=\int \rho r^2 dV \]
其中 \(\rho\) 是密度, \(dV\) 是微元的体积。
转动动能
在直线运动中,物体的动能是:\(K=\frac{1}{2} mv^2\) ,在转动中, \(v=\omega r\) 且 \(m=\int \rho dV\),则: \[ K= \frac{1}{2} \int \rho \omega r^2 dV = \frac{1}{2} \left(\int \rho r^2 dV \right)\omega^2 \]
\[ K=\frac{1}{2} I \omega^2 \]
转动惯量列表
| 描述 | 示意图 | 转动惯量 |
|---|---|---|
| 质点 |  |
\(I=mr^2\) |
| 细棒-绕中心 |  |
\(I_{center}=\frac{1}{12}mL^2\) |
| 细棒-绕端点 |  |
\(I_{end}=\frac{1}{3}mL^2\) |
| 细圆环 |  |
$I_z=mr^2 $ |
| \(I_x=I_y=\frac{1}{2}mr^2\) | ||
| 圆盘 |  |
\(I_z=\frac{1}{2}mr^2\) |
| \(I_x=I_y=\frac{1}{4}mr^2\) | ||
| 环形圆盘 |  |
\(I_z=\frac{1}{2}m(r_1^2+r_2^2)\) |
| \(I_x=I_y=\frac{1}{4}m(r_1^2+r_2^2)\) | ||
| 圆柱壳 | 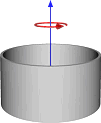 |
\(I\approx mr^2\) |
| 圆柱 |  |
$I_z=mr^2 $ |
| 圆柱 | center | \(I_x=I_y=\frac{1}{12}m(3r^2+h^2)\) |
| 圆柱 | end | \(I_x=I_y=\frac{1}{12}m(3r^2+4h^2)\) |
| 空心圆柱 |  |
\(I_z=\frac{1}{2}m(r_1^2+r_2^2)\) |
| 空心圆柱 | center | \(I_x=I_y=\frac{1}{12}m(3(r_1^2+r_2^2)+h^2)\) |
| 空心圆柱 | end | \(I_x=I_y=\frac{1}{12}m(3(r_1^2+r_2^2)+4h^2)\) |
| 长方体 | 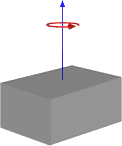 |
$I_h=m(w2+d2) $ |
| $I_w=m(d2+h2) $ | ||
| \(I_d=\frac{1}{12}m(w^2+h^2)\) |
截面惯性矩
概念
截面惯性矩又称面积二次轴矩=横截面的惯性矩=面积惯性矩 (英语:second moment of aera, second aera mement, quadratic moment of aera, aera moment of inertia) 通常是对受弯曲作用物体的横截面而言,是反映截面的形状与尺寸对弯曲变形影响的物理量。弯曲作用下的变形或挠度不仅取决于荷载的大小,还与横截面的几何特性有关。如工字梁的抗弯性能就比相同截面尺寸的矩形梁好。它和反映截面抗扭转作用性能的面积极惯性矩是相似的。
定义
截面的面积为 \(A\),则: \[ I_x = \int_A y^2 dA=\int \int y^2 dx dy \]
\[ I_y = \int_A x^2 dA=\int \int x^2 dx dy \] 分别表示截面对坐标轴\(x\)与\(y\)的惯性矩,第一式中的 \(y\) 和第二式中的 \(x\) 分别表示面积微元 \(dA\) 到 \(x\) 和到 \(y\) 轴的垂直距离。
截面惯性矩列表(含极惯性矩)
| 描述 | 示意图 | 截面惯性矩 |
|---|---|---|
| 圆 |  |
\(I_x=I_y=\frac{\pi}{4}r^4\) |
| \(I_z=\frac{\pi}{4}r^4\) | ||
| 圆环 |  |
\(I_x=I_y=\frac{\pi}{4}(r_2^4-r_1^4)\) |
| \(I_z=\frac{\pi}{2}(r_2^4-r_1^4)\) | ||
| 长方形-中心 |  |
\(I_x=\frac{bh^3}{12}\) |
| \(I_y=\frac{b^3h}{12}\) | ||
| \(I_z=\frac{b^3h+bh^3}{12}\) | ||
| 长方形-端点 |  |
\(I_x=\frac{bh^3}{3}\) |
| \(I_y=\frac{b^3h}{3}\) | ||
| \(I_z=\frac{b^3h+bh^3}{3}\) | ||
| 长方形-空心 |  |
\(I_x=\frac{bh^3-b_1h_1^3}{12}\) |
| \(I_y=\frac{b^3h-b_1^3h_1}{12}\) | ||
| 三角形-形心 |  |
\(I_x=\frac{bh^3}{36}\) |
| \(I_y=\frac{b^3h-b^2ha+bha^2}{36}\) | ||
| 三角形-端点 |  |
\(I_x=\frac{bh^3}{12}\) |
| \(I_y=\frac{b^3h+b^2ha+bha^2}{12}\) |
极惯性矩
概念
极惯性矩又称截面二次极矩 (英语:second polar moment of aera, polar moment of inertia) 通常是对受扭转作用物体的横截面而言,是反应截面形状与尺寸对扭转变形影响的物理量。通常用 \(I_z\) 或 \(I_p\) 表示。
定义
截面的面积为 \(A\),且面积微元 \(dA\) 到 \(z\) 轴的距离为 \(\rho\) 则: \[ I_z = \int_A \rho^2 dA=\int \int x^2+y^2 dx dy \]
截面惯性矩与极惯性矩的关系为:
\[ I_z = \int_A \rho^2 dA=\int \int y^2+x^2 dx dy = I_x + I_y \]
三者的区别
- 转动惯量:转动惯量越大,惯性越大,物体旋转越难改变(需要的力矩越大)与质量分布有关;
- 截面惯性矩:截面惯性矩越大,物体越难弯曲,抗弯截面模量也越大。与质量分布无关。
- 极惯性矩:极惯性矩越大,物体越难扭转。与质量分布无关。与截面惯性矩的关系为: \(I_z=I_x+I_y\)。