通俗的理解何为变分
概述
我们可以从微分的概念出发理解变分。
微分:设有一个自变量 \(x\in(a,b)\) ,这个自变量的微小变化量记为 \(\mathrm{d}x\),称为微分。此时我们关心的是,当自变量有微小变化 (\(\mathrm{d}x\)) 时,函数 (\(y(x)\)) 变化了多少。
变分:设有一个函数(泛函) \(I=G(y,y^{\prime})\),其中 \(y=y(x)\) 是另一个函数(定义在某一个函数空间内是不确定的)。这个函数 \(y\) 的微小变化量记为 \(\delta y\),称为变分。此时我们关心的是,当函数 \(y\) 有微小变化时,函数(泛函) \(I\) 变化了多少。
简而言之,变分就是微分在函数空间的拓展,其精神内涵是一致的。
泛函:是将函数空间(无限维空间)映射到数域,就是把一个函数映射成一个数。打个比方,从A点到B点有无数条路径,每一条路径都是一个函数。这无数条路径,每一条函数(路径)的长度都是一个数。从这无数个路径当中选一个路径最短或者最长的,就是求泛函的极值问题。
变分
假设我们有两个定点 \((a,p)\) 和 \((b,p)\),连接这两点的任意曲线的方程 \(y=y(x)\) 都将满足如下的边界条件:
\[ y(a)=p,\quad y(b)=q \]
现在考虑如下形式的定积分:
\[ I=\int_{a}^{b} f\left(y, y^{\prime}\right) \mathrm{d} x \]
其中 \(f(y, y^{\prime})\) 是关于 \(y(x)\) 和它的一阶导数 \(y^{\prime}(x)\) 的函数,在实际问题中,我们有时需要找到一个具体的 \(y(x)\) 使得 \(I\) 有极值。
注意在一般的极值问题中,我们考察的是自变量 \(x\) 的变化:\(x\) 取值多少时,函数会有极值。这个新问题的不同之处在于,我们考察的是函数 \(y(x)\) 的变化:\(y(x)\) 是什么形式时,\(I\) 会有极值(\(I\) 称作函数 \(y(x)\) 的泛函)。然而这两类问题依然有共通之处:当 \(I\) 取极值时,对 \(y(x)\) 作微小的变化,\(I\) 在一级近似下应该保持不变。
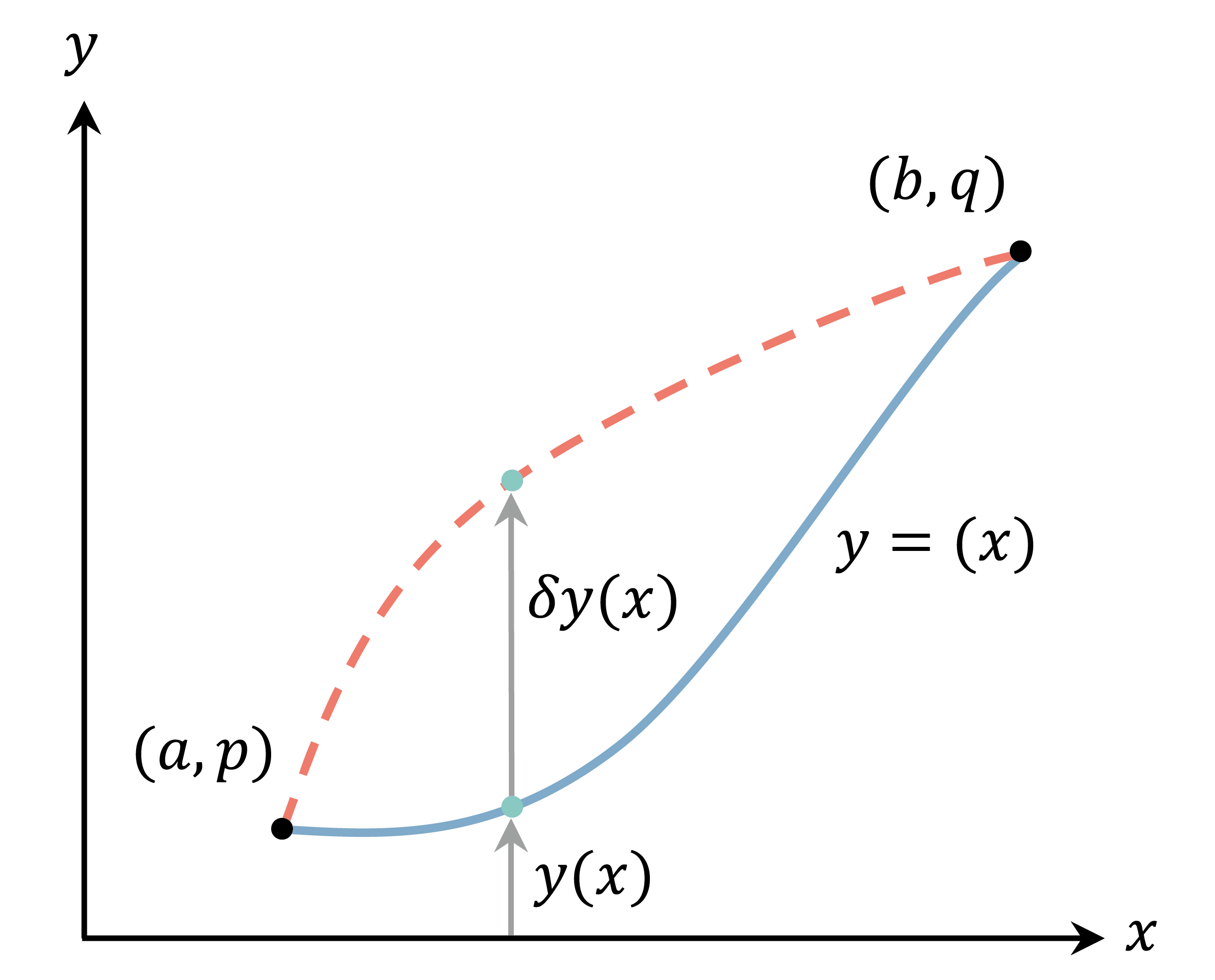
如果 \(y(x)\) 有微小改变 \(\delta y(x)\)(高大上叫法:\(\delta y(x)\) 称作函数 \(y(x)\) 的变分),那么 \(f\left(y, y^{\prime}\right)\) 的变化为:
\[ \delta f=\frac{\partial f}{\partial y} \delta y+\frac{\partial f}{\partial y^{\prime}} \delta y^{\prime} \]
\(I\) 相应的变化为:
\[ \delta I=\int_{a}^{b}\left[\frac{\partial f}{\partial y} \delta y+\frac{\partial f}{\partial y^{\prime}} \delta y^{\prime}\right] \mathrm{d} x \]
方括号里的第二项可以改写成 \(\frac{\partial f}{\partial y^{\prime}} \frac{\mathrm{d}(\delta y)}{\mathrm{d} x}\),然后可以进行分部积分:
\[ \int_{a}^{b} \frac{\partial f}{\partial y^{\prime}} \delta y^{\prime} \mathrm{d} x =\int_{a}^{b} \frac{\partial f}{\partial y^{\prime}} \mathrm{d}(\delta y) = \frac{\partial f}{\partial y^{\prime}} \delta y {\bigg|} _{a} ^{b} -\int _{a} ^{b} \delta y \frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{\partial f}{\partial y^{\prime}}\right) \mathrm{d} x \]
由于 \(y(x)\) 的边界条件固定,\(\delta y(a)=\delta y(b)=0\),所以分部积分出来的第一项为零,仅第二项有贡献。上式化简为:
\[ \delta I=\int_{a}^{b}\left[\frac{\partial f}{\partial y}-\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial f}{\partial y^{\prime}}\right)\right] \delta y(x) \mathrm{d}x \]
如果 \(I\) 有极值,对任意满足边界条件的 \(\delta y(x)\) 都必须有 \(\delta I=0\),这就要求:
\[ \frac{\partial f}{\partial y}-\frac{\mathrm{d}}{\mathrm{d} x}\left(\frac{\partial f}{\partial y^{\prime}}\right)=0 \]
这便是 Euler-Lagrange 方程,它是变分法的核心定理。有了它,原则上就可以找出所寻求的极值函数 \(y(x)\)。
Euler-Lagrange 方程的应用:两点间最短路径问题、最速降曲线问题、悬链线等。
本文参考了以下博主分享的文章: * 浅谈变分原理 * 微分、差分和变分的概念有什么异同?