最小势能原理与最小余能原理
概述
最小势能原理和最小余能原理是物理和工程学中的基本概念,被应用于力学、电学、生物学等多种学科。
弹性力学有两种提法,一种微分提法,一种变分提法。微分提法从微元入手,得到严格满足方程和边界条件的强解;变分提法从整体(能量)入手,得到弱解。最小势能原理和最小余能原理是为后者服务的,它们从能量入手,为一些经典方法的提出奠定了理论基础,如Galerkin(伽辽金)方法、Rayleigh–Ritz(瑞利-里兹)方法等。本文只讨论弹性力学中的最小势能原理与最小余能原理。
为了阐明这两种原理及其关系,需要引入一些概念:运动许可状态、静力许可状态、虚位移、虚力、系统的总势能、系统的总余能、应变能密度、余应变能密度、可能功原理。
相关概念的引入
基本概念
- 运动许可状态: 满足位移约束条件的(可能存在的)状态。相应的变分是虚位移。
- 静力许可状态: 满足平衡方程和力边界条件的(可能存在的)状态。相应的变分是虚力。
- 虚位移: 给定的瞬时和位形上,虚位移是符合约束条件的无穷小位移。
- 虚力: 给定的瞬时和位形上,虚力是符合平衡方程和力边界条件的的无穷小力。
- 总势能 \(\Pi\): 等于应变能+外力势(\(\Pi=U+W\))
- 总余能 \(\Pi^*\): 等于余应变能+外力余势(\(\Pi ^ * = U ^ *+ W ^ *\))
应变能、余应变能、外力势、外力余势的概念见下一节
应变能和余应变能
应变能: 弹性体受外力作用产生应变,产生应力场和位移场。外力对弹性体所做的功以变形能的形式储存在弹性体内,这种变形能通常称为应变能。
现以杆件的拉伸问题为例介绍应变能和余应变能的概念。如下图(a)所示,杆件原长为 \(l\),伸长量为 \(u=\varepsilon l\),受到一个平行于杆件的静力 \(P=\sigma f\),\(f\) 为横截面积。
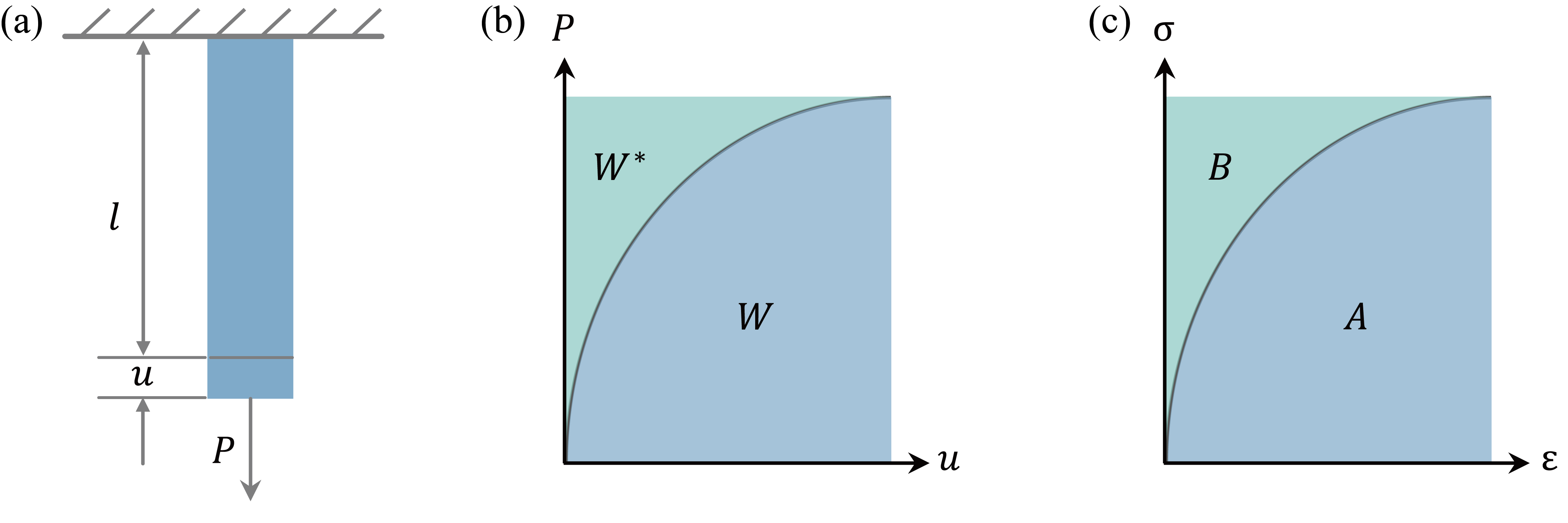
此时,外力 \(P\) 所做的功所引起的势能损失为图(b)中曲线下半部分面积 \(W\),被称为外力势(外载荷的势能):
\[ W= -\int _0^u P \mathrm{d} u = -fl \int _0^\varepsilon \sigma \mathrm{d} \varepsilon \]
上式中的正负号表示外力所做的功引起的系统势能的增减,此时外力方向与位移方向相同,外力做正功,系统有势能损失,为负号。这可能不好理解,那么我们考虑重力对物体的影响。当一个重物被抬升一段距离,此时系统势能增加,重力做负功。即外力方向与位移方向相反,外力做负功,系统势能增加。
画出系统的应力应变曲线图(c),则上式左端
\[ A = \int _0^\varepsilon \sigma \mathrm{d} \varepsilon \]
代表单位体积下的应变势能,定义为应变能密度。则系统的应变能 \(U\) 为:
\[ U= \int _V A \mathrm{d}V = fl \int _0^\varepsilon \sigma \mathrm{d} \varepsilon \]
与应变能相对的是余应变能。
| 应变能 \(U\) | 余应变能 \(U^*\) |
|---|---|
| 应变能密度 \(A\) | 余应变能密度 \(B\) |
| 外力势 \(W\) | 外力余势 \(W^*\) |
余应变能密度 \(B\) 对应图(c)上半部分面积:
\[ B = \int _0^\sigma \varepsilon \mathrm{d} \sigma \]
则系统的余应变能 \(U^*\) 为:
\[ U= \int _V B \mathrm{d}V = fl \int _0^\sigma \varepsilon \mathrm{d} \sigma \]
外力余势 \(W^*\) 对应图(b)上半部分面积:
\[ W^* = -\int _0^P u \mathrm{d} P \]
外力余势通常在支撑部分。
应变能与余应变能之间的关系:
\[ A+B = \int _V \sigma \varepsilon \mathrm{d} V \]
可能功原理
考虑弹性体的两个状态,状态一是应力许可的,状态二是运动许可的。
利用上标 \(s\) 表示状态一(\(f _i\) 为体力,\(p _i\) 为面力)
\[ \sigma _{ij,j}^{(s)}+ f _i^{(s)}=0 \]
\[ \sigma _{ij}^{(s)} v _j =p _i^{(s)} \]
利用上标 \(k\) 表示状态二
\[ \varepsilon _{ij}^{(k)} = \frac{1}{2} \left( u _{i,j}^{(k)} + u _{j,i}^{(k)} \right) \]
考虑状态一中的体力、面力和可能应力在状态二的相应可能位移和可能应变上所做的功,分别为:
\[ A _f = \int _V f _i^{(s)} u _i^{(k)} \mathrm{d} V \]
\[ A _p = \int _S p _i^{(s)} u _i^{(k)} \mathrm{d} S = \int _S \sigma _{ij}^{(s)} u _i^{(k)} v _j \mathrm{d} S = \int _V \left( \sigma _{ij}^{(s)} u _i^{(k)} \right) _{,j}\mathrm{d} V = \int _V \sigma _{ij,j}^{(s)} u _i^{(k)} \mathrm{d} V +\int _V \sigma _{ij}^{(s)} u _{i,j}^{(k)} \mathrm{d} V \]
\[ A _\sigma = \int _V \sigma _{ij}^{(s)} \varepsilon _{ij}^{(k)} \mathrm{d} V \]
可能功原理: 外力功等于内力功,状态一的外力在状态二位移做的功等于状态一的应力在状态二的应变上做的功。
物理意义: 外力与内力构成自平衡力系,他们在可能位移上做的总功为零。 适用性: 静力可能状态和几何可能状态时完全独立的;与本构关系无关,适用于任何连续介质
推导过程如下:
\[ A _p = \int _V \sigma _{ij,j}^{(s)} u _i^{(k)} \mathrm{d} V +\int _V \sigma _{ij}^{(s)} u _{i,j}^{(k)} \mathrm{d} V = \int _V f _i^{(s)} u _i^{(k)} \mathrm{d} V + \int _V \sigma _{ij}^{(s)} \varepsilon _{ij}^{(k)} \mathrm{d} V = -A _f +A _\sigma \]
\[ A _f + A _p = A _\sigma \]
\[ \int _V f _i^{(s)} u _i^{(k)} \mathrm{d} V + \int _S p _i^{(s)} u _i^{(k)} \mathrm {d} S = \int _V \sigma _{ij}^{(s)} \varepsilon _{ij}^{(k)} \mathrm{d} V \]
最小势能原理
原理简述
最小势能原理: 在满足弹性体的几何方程和位移边界条件的所有容许的位移中,真实的位移必使弹性体的总势能有驻值。当弹性体为稳定平衡时,其总势能为极小值。
简述为:在一切运动许可状态中,真实状态的总势能最小。
原理推导
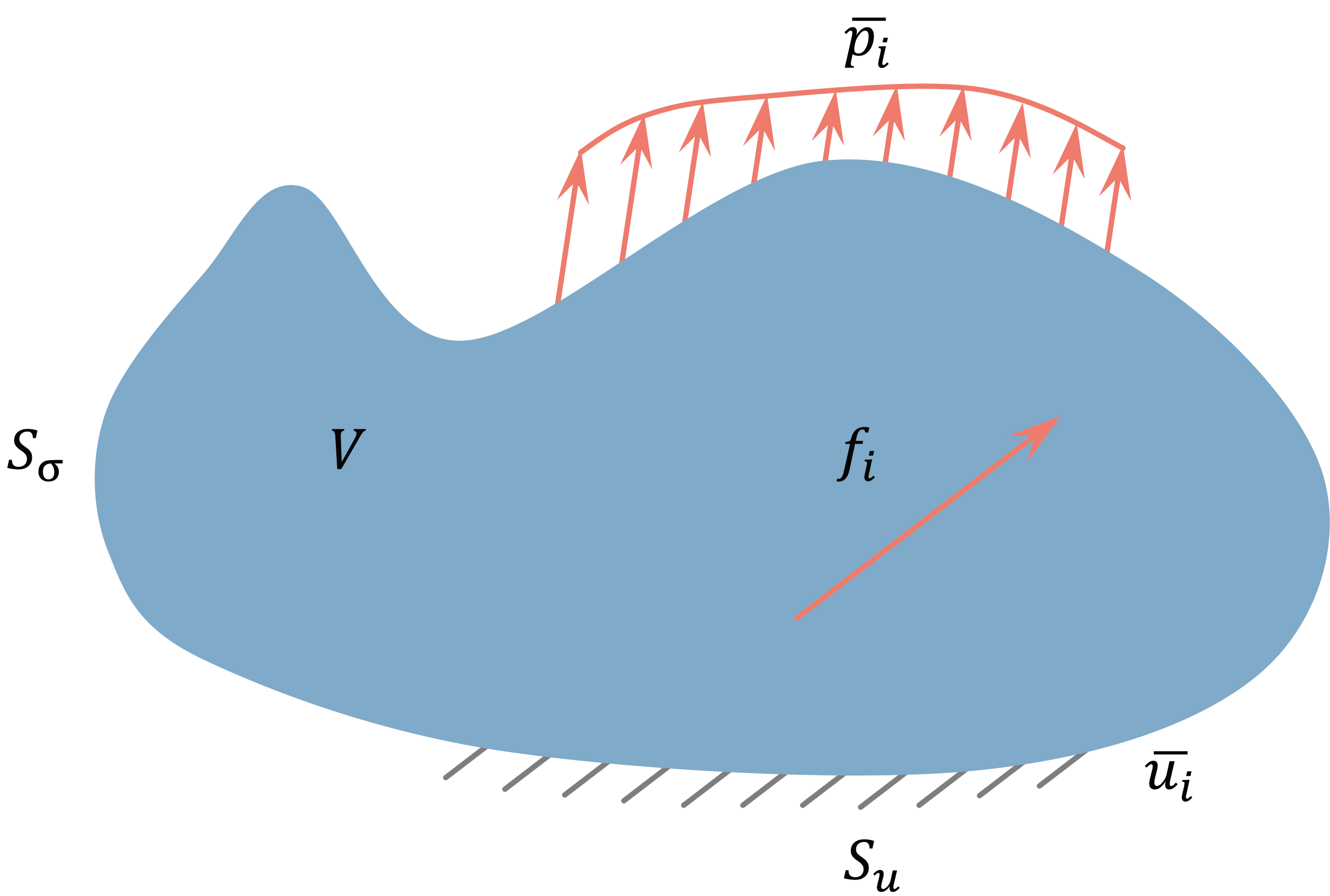
图中是一个一般意义下的弹性体。受到的外力分为面力 \(\bar{p} _i\) 和体力 \(f _i\);弹性体的外表面 \(S _u\) 所在区域受到位形约束 \(\bar{u} _i\)。
\[ \varepsilon _{i j}=\frac{1}{2}\left(u _{i, j}+u _{j, i}\right) \]
\[ \sigma _{i j, j}+f _{i}=0 \]
\[ \sigma _{i j} v _{i}=\bar{p} _{j} \quad \text { on } S _{\sigma} \]
\[ u _{i}= \bar{u} _{i} \quad \text { on } S _{u} \]
\[ \sigma _{i j}=\frac{\partial A\left(\varepsilon _{i j}\right)}{\partial \varepsilon _{i j}} \]
真实状态的总势能 \(\Pi\) 分为应变能 \(U\) 和 外力势 \(W\) 两部分:
\[ \Pi = U+W = \int _{V} A \left( \varepsilon _{i j} \right) \mathrm{d} V- \left( \int _{V} f _{i} u _{i} \mathrm{d} V+\int _{S _{\sigma}} \bar{p} _{i} u _{i} \mathrm{d} S \right) \]
其中 \(A(\varepsilon_{ij})\) 为应变能密度。
运动许可状态由 \(\varepsilon _{ij} ^{(k)}\) 和 \(u _{i} ^{(k)}\) 描述,仅满足变形关系:
\[ \varepsilon_{i j}^{(k)}=\frac{1}{2}\left(u_{i, j}^{(k)}+u_{j, t}^{(k)}\right), \quad u_{i}^{(k)}=\bar{u}_{i} \]
运动许可状态的总势能为:
\[ \Pi^{(k)}=\int _{V} A^{(k)}\left(\varepsilon _{i j}^{(k)}\right) \mathrm{d} V-\int _{V} f _{i} u _{i}^{(k)} \mathrm{d} V-\int _{S _{\sigma}} \bar{p} _{i} u _{i}^{(k)} \mathrm{d} S \]
两种状态的总势能差为:
\[ \begin{aligned} \Pi^{(k)}-\Pi &=\int_{V}\left[A^{(k)}\left(\varepsilon_{i j}^{(k)}\right)-A\left(\varepsilon_{i j}\right)\right] \mathrm{d} V \\ &-\int_{V} f_{i}\left[u_{i}^{(k)}-u_{i}\right] \mathrm{d} V-\int_{S} p_{i}\left[u_{i}^{(k)}-u_{i}\right] \mathrm{d} S \end{aligned} \]
注意到与面力相关项的积分区域 \(S_\sigma \rightarrow S\),这是因为两种状态都满足位形约束,所以两种状态在 \(S _u\) 的位移差恒为0。
利用可能功原理,外力项可以被改写为:
\[ -\int_{V} f_{i}\left[u_{i}^{(k)}-u_{i}\right] \mathrm{d} V-\int_{S} p_{i}\left[u_{i}^{(k)}-u_{i}\right] \mathrm{d} S =-\int_{V} \sigma_{i j}\left(\varepsilon_{i j}^{(k)}-\varepsilon_{i j}\right) \mathrm{d} V=-\int_{V} \frac{\partial A}{\partial \varepsilon_{i j}}\left(\varepsilon_{i j}^{(k)}-\varepsilon_{i j}\right) \mathrm{d} V \]
则两种状态的势能差为:
\[ \Pi^{(k)}-\Pi=\int_{V}\left[A^{(k)}\left(\varepsilon_{i j}^{(k)}\right)-A\left(\varepsilon_{i j}\right) - \frac{\partial A}{\partial \varepsilon_{i j}}\left(\varepsilon_{i j}^{(k)}-\varepsilon_{i j}\right)\right] \mathrm{d} V \]
只要应变能密度函数 \(A\) 是凸函数,则必有:
\[ \Pi^{(k)}-\Pi \geq 0 \]
最小势能原理的变分形式:
\[ \delta \Pi=0 \]
\[ \delta \Pi=\delta U+\delta V=\delta \int _{V} A \mathrm{d} V-\int _{V} f _{i} \delta u _{i} \mathrm{d} V-\int _{S _{\sigma}} \bar{p} _{i} \delta u _{i} \mathrm{d} S \]
\[ \delta U=-\delta V=\int _{V} f _{i} \delta u _{i} \mathrm{d} V+\int _{S _{\sigma}} \bar{p} _{i} \delta u _{i} \mathrm{d} S \]
最小余能原理
原理简述
最小势能原理: 在弹性体内满足平衡微分方程,在应力边界上满足应力边界条件的所有容许的应力状态中,真实的应力状态(满足变形协调条件的应力)必使其总余能为极小值。
简述为:在一切静力许可状态中,真实状态的总余能最小。
原理推导
还是考虑上图中的弹性体,应变可以用余应变能 \(B\) 表示:
\[ \varepsilon_{i j}=\frac{\partial B\left(\sigma_{i j}\right)}{\partial \sigma_{i j}} \]
真实状态的系统总余能 \(\Pi^*\) 由 余应变能 \(U^*\) 和外力余势 \(W^*\) 构成:
\[ \Pi ^*= U^* +W^* \int_{V} B \left(\sigma_{i j}\right) \mathrm{d} V- \int_{S_{u}} p_{i} \bar{u}_{i} \mathrm{~d} S \]
静力许可状态仅满足静力关系:
\[ \sigma _{i j, j}^{(s)}+f _{i}=0 \quad \text{ on } V \]
\[ p_{i}^{(s)}=\sigma_{i j}^{(s)} v_{j} \quad \text{ on } S _u \]
\[ p_{i}^{(s)}=\bar{p}_{i}\quad \text{ on } S _\sigma \]
静力许可状态的总余能为:
\[ \Pi ^{*(s)}= \int_{V} B^{(s)}\left(\sigma_{i j}^{(s)}\right) \mathrm{d} V- \int_{S_{u}} p_{i}^{(s)} \bar{u}_{i} \mathrm{~d} S \]
两种状态的势能差为:
\[ \Pi^{* (s)}-\Pi^*= \int _{V}\left[B^{(s)} \left( \sigma _{ij}^{(s)} \right)-B\left(\sigma _{i j}\right)\right] \mathrm{d} V -\int _{V}\left(f _{i}^{(s)}-f _{i}\right) u _{i} \mathrm{d} V-\int _{S}\left(p _{i}^{(s)}-p _{i}\right) u _{i} \mathrm{d} S \]
利用可能功原理,外力项可以被改写为:
\[ -\int _{V} \left( f _{i}^{(s)}-f _{i}\right) u _{i} \mathrm {d} V-\int _{S}\left(p _{i}^{(s)}-p _{i}\right) u _{i} \mathrm {d} S=-\int _{V} \varepsilon _{i j} \left( \sigma _{i j}^{(s)}-\sigma _{i j}\right) \mathrm {d} V =-\int _{V} \frac {\partial B}{\partial \sigma _{i j}}\left(\sigma _{i j}^{(s)}-\sigma _{i j}\right) \mathrm {d} V \]
只要应变余能密度函数 \(B\) 是凸函数,则必有:
\[ \Pi^{* (s)}-\Pi^* \geq 0 \]
最小势能原理和最小余能原理的区别与联系
联系:
\[ \Pi+\Pi^* =\int _{V} \left[ A+B \right] \mathrm{d} V-\int _{V} f _{i} u _{i} \mathrm{d} V-\int _{S _{\sigma}} \bar{p} _{i} u _{i} \mathrm{d} S-\int _{S _{u}} p _{i} \bar{u} _{i} \mathrm{d} S =\int _{V} \sigma _{i j} \varepsilon _{i j} \mathrm{d} V-\int _{V} f _{i} u _{i} \mathrm{d} V-\int _{S} p _{i} u _{i} \mathrm{d} S \]
由可能功原理可得 \(\Pi +\Pi^*=0\)。
于是有:
\[ \Pi^{* (s)} \geq \Pi^* =-\Pi \geq - \Pi^{(k)} \]
因此用这两种原理建立数值方程求解有如下特点: * 利用最小势能原理求得位移近似解的弹性变形能是精确解变形能的下届,即近似的位移场在总体上偏小,也就是说结构的计算模型显得偏于刚硬。 * 利用最小余能原理得到的近似解的弹性余能是精确余能的上界,即近似的应力解在总体上偏大,结构计算模型模型偏于柔软。 * 分别利用这两个极值原理求解同一个问题时,可以获得这个问题的上界和下界,可以较准确的估算所得近似解的误差。
区别: 最小势能原理以位移为基本变量,要求位移场事先满足几何方程和给定位移边界条件。最小余能原理以应力为基本变量,要求应力场事先满足平衡方程和给定面力边界条件。
用这两个原理求解的优点是通常只有一个场函数,且泛函具有极值性。但是对于许多物理或力学问题,要求场函数事先满足全部附加条件是很困难的。