采样定理
采样
采样就是将连续模拟信号变为离散数字信号的过程。
什么是采样定理
离散后的信号能唯一的确定原连续信号,并要求离散信号通过D/A(数/模)转化后能恢复成原连续信号。由于离散信号是从连续信号上取出的一部分值,与连续信号的关系是整体和局部的关系,一般来说是不可能唯一确定连续信号的。只有在满足一定条件下,离散信号才可按照一定方式恢复出原来的连续信号。这个条件就是采样定理。
如何满足采样定理
采样定理:采样频率必须大于被分析信号成分中最高频率值的两倍以上,否则将产生高、低频混淆现象,即高频信号经采样后只出现低频信号,采样信号无法还原为原信号。 \[ f_s=\frac{1}{\Delta t} >2f_m \]
其中\(f_s\)是采样频率,\(f_m\)是被分析信号成分中的最高频率值,\(\Delta t\)是采样时间间隔。
频率混淆现象
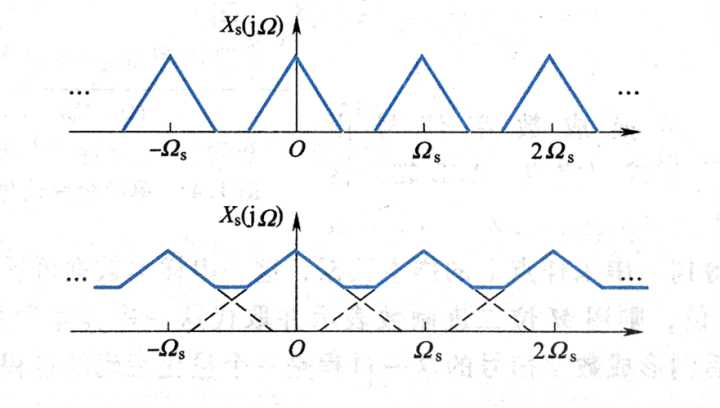
如果想彻底了解采样定理的内涵,以及为什么不满足采样定理就会出现混淆现象,请接着看下去 读者自己推导采样后得到的信号\(x_s(t)\)的傅里叶变换表达式\(X_s(j\omega)\),再根据\(X_s(j\omega)\)绘制频谱图,最终就会理解采样定理的内涵。
为了便于推导,现定义: * 原信号:\(x_m(t)\),傅里叶变换后为\(X_m(j\omega)\) * 采样函数:\(s(t)\),傅里叶变换后为\(S(j\omega)\) * 采样后输出信号:\(x_s(t)\),傅里叶变换后为\(X_s(j\omega)\)
采样函数\(s(t)\)
当我们把采样的过程看作一个周期为 \(T\) 、宽度为 \(\tau\) 的矩形脉冲信号\(s(t)\)。当\(\tau\ll T\) 时,采样脉冲信号\(s(t)\)具有了狄拉克\(\delta\)函数的性质:
\[ \delta(t)= \begin{cases} \infty & t=0 \\\\ 0 & t\neq 0 \end{cases} \]
\[ s(t)= \sum^\infty_{n=-\infty} \delta(t-nT) \]
为了便于傅里叶变换,把\(s(t)\)表示为傅里叶级数的形式:
\[ s(t)=\sum^\infty_{k=-\infty} a_k e^{jk\omega_s t} ,\quad \omega_s=\frac{2\pi}{T} \]
其中:
\[ a_k=\frac{1}{T} \int^{T/2}_ {-T/2} \sum\nolimits^\infty_{n=-\infty} \delta(t-nT) e^{-j\omega_s t} dt=\frac{1}{T} \]
因此,有:
\[ s(t)=\frac{1}{T} \sum^\infty_{k=-\infty} e^{jk\omega_s t} \]
对\(s(t)\)进行傅里叶变换得到\(S(j\omega)\):
\[ S(j\omega)=F \left[ s(t) \right] =F \left[ \frac{1}{T} \sum^\infty_{k=-\infty} e^{jk\omega_s t} \right] = \frac{1}{T} \sum^\infty_{k=-\infty} F \left[ e^{jk\omega_s t} \right] \]
查常用Fourier变换表可知:
\[ F \left[ e^{jk\omega_s t} \right] =2\pi \delta(\omega -k\omega_s) \]
则\(S(j\omega)\)为:
\[ S(j\omega) = \frac{2\pi}{T} \sum^\infty_{k=-\infty} \delta(\omega -k\omega_s) \]
采样后输出的信号\(x_s(t)\)
采样后输出的信号\(x_s(t)\)等于原信号\(x_m(t)\)乘采样函数\(s(t)\):
\[ x_s(t)=x_m(t)s(t) \]
记\(*\)为卷积,根据频域下的卷积定理
\[ f_1(t)f_2(t)=\frac{1}{2\pi}F^{-1}\left[ F_1(j\omega)* F_2(j\omega)\right] \]
采样后输出的信号\(X_s(j\omega)\)为:
\[ X_s(j\omega)=\frac{1}{2\pi} X_m(j\omega)*S(j\omega)=\frac{1}{2\pi}· X_m(j\omega) *\left[ \frac{2\pi}{T} \sum^\infty_{k=-\infty} \delta(\omega -k\omega_s) \right] \]
根据冲击函数的性质有: \[ X_s(j\omega)=\frac{1}{T} \int^\infty _ {-\infty} X_m(j\theta) \sum^\infty_{k=-\infty} \delta(\omega -k\omega_s - \theta) d\theta \]
冲激函数的性质:\(f(t)*\delta(t-t_0)=f(t-t_0)\)
最终,采样后信号的傅里叶变换为:
\[ X_s(j\omega)=\frac{1}{T}\sum^\infty_{k=-\infty} X_m(j\omega-jk\omega_s) \]
从上式可以看出,原信号的频谱\(X_m(j\omega)\)在频域内发生了周期延拓。即,原信号在频谱上的宽度是\(2f_m\),每隔\(f_s\)重复一次(相当于信号的平移),发生了周期延拓,从图中直观的看出来,如果\(f_s<2f_m\),延拓后的信号会在频域内会发生混淆。